Overview and Objective
In this lesson, students will explore the artistic style of Piet Mondrian while working on the Mondrian Art Puzzle by Gordon Hamilton.
Warm-Up
You may start by introducing Piet Mondrian and his famous artworks.
Abstract art usually does not show recognizable things such as people, objects, or landscapes. Instead, artists use colors, shapes, and textures on their canvasses. Dutch artist Piet Mondrian (1872–1944) is one of the best-known abstract painters. His abstract style is mostly based on simple geometric elements, the three primary colors (red, blue, and yellow), the three primary values (black, white, and gray). He had an enormous influence on 20th-century art including design, architecture, and fashion. Invite students to explore his art in more detail if they are interested.

When Mondrian made his paintings, he would always mix his own colors, never using the paint directly out of a tube. Here are the rectangles with the closest hues to the Mondrian colors. Invite students to open this Polypad to create their first Mondrian-like art by resizing the given rectangles to fit in a 5 x 5 square canvas.
Main Activity
Invite students to share their art pieces with the class. Discuss the area of the 5x5 canvas and the rectangles they have created. Next, invite students to create a second art piece. However, now students are only allowed to use rectangles with different dimensions.
For example, if students create a 3 x 4 rectangle, they cannot create another 3 x 4 or 4 x 3 rectangles on the same canvas. However, they can create a 2 x 6 rectangle on the same canvas, and other rectangles with different areas. Allow students some time to complete their second art piece. After having them share their examples, ask about the areas of the rectangles they have created.
Ask students to determine the difference between the largest area and the smallest area they have created on their canvas. Explain to them that this value will be the Mondrian Art Score they will be working on during this activity.
You may give one example to demonstrate the calculation of the score and ask students to calculate the scores of the other size canvasses in this example.
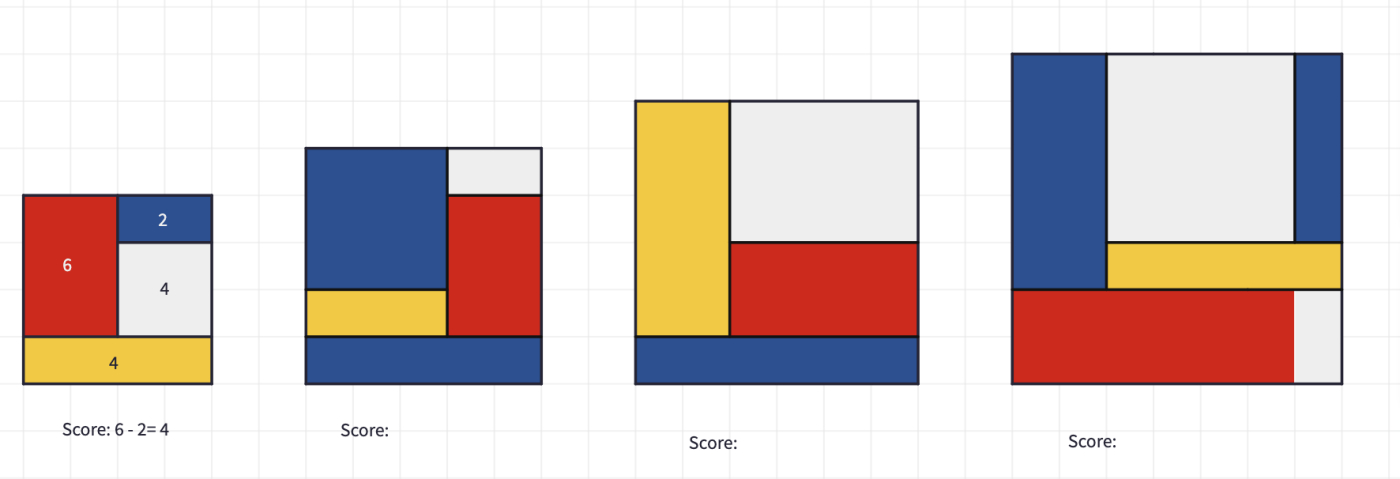
- 4 by 4 canvas has a Mondrian Score of 4.
- 5 by 5 canvas has a Mondrian Score of 7.
- 6 by 6 canvas has a Mondrian Score of 6.
- 7 by 7 canvas has a Mondrian Score of 14.
Tell students that the lowest possible score of a 4 by 4 canvas is actually 4. There can be different designs that come up with the same lowest score but not less!
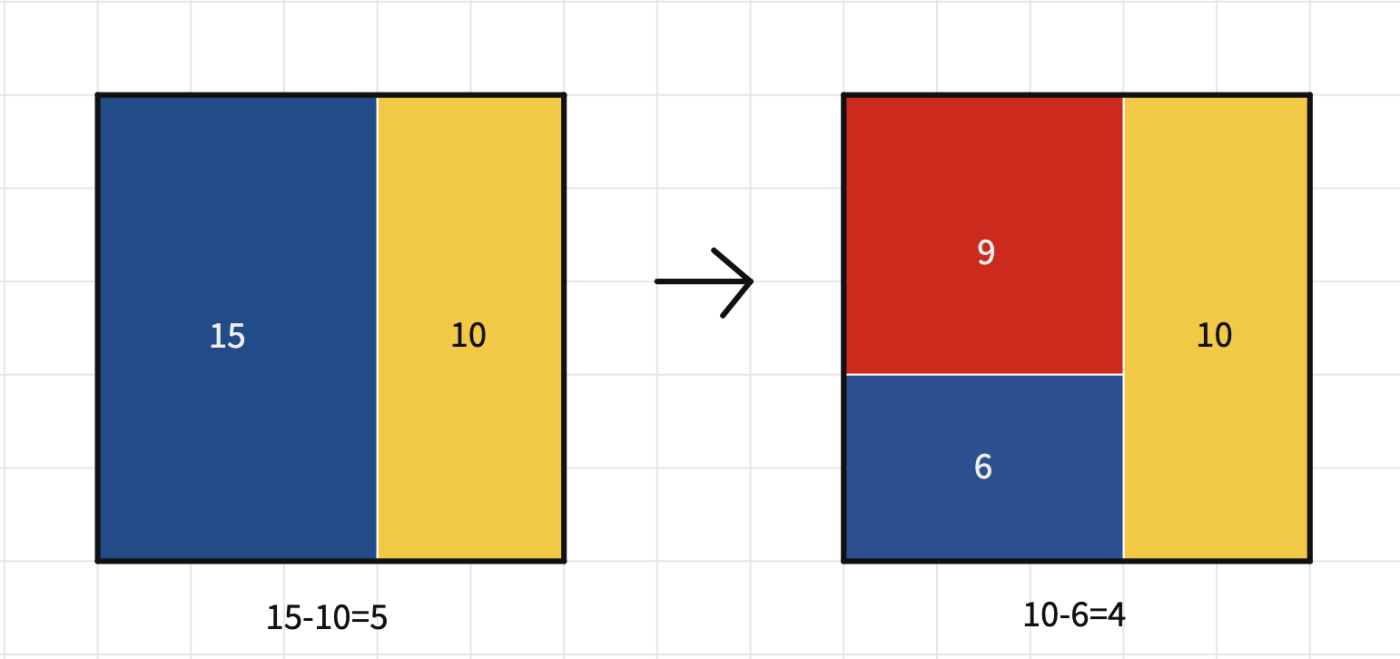
However, for the 5 by 5 canvas, the score can be improved by changing the design. If needed (and according to the students’ grade level), you may discuss the possible strategies to lower the score as a class.
You may start by dividing the 5x5 square into two parts as 3x5 and 2x5. Here the score is 5. It is a low score but we may continue to look for a lower one by decomposing the big area into two again. We now have a score of 4 which is actually the lowest score for a 5 x 5 canvas.
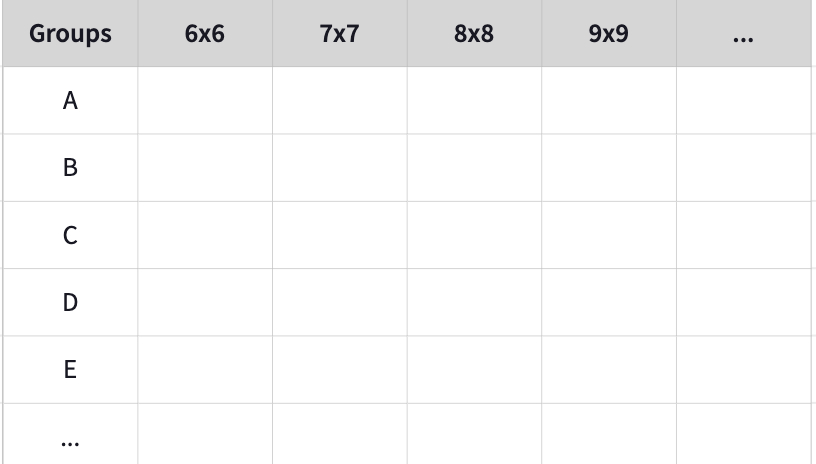
Share this Polypad with the students and have them work in pairs to find the lowest scores for different sizes of canvasses. Clarify with the students that the goal of this puzzle is to have the Mondrian score, “the difference of the largest area and smallest area “ as small as possible while having no rectangles with the same dimensions.
You can record and display the scores for each size of the canvas on the board to create a competitive atmosphere among the groups. Remind students to ask each other the ways to improve their results.
Share some student work with the class. Invite students to share which approaches they found most useful when creating the lowest score. To close the lesson, discuss as a class
- What specific strategies did they use to find the lowest possible score?
- Do they think they could find a lower score?
- Does the Mondrian Score get bigger with the increasing size of the square canvasses?
- Do they see any pattern among the scores?
Closure
To close the activity, share with students that no pattern or structure has been identified in the solutions of this puzzle. The actual algorithm for solving Mondrian art puzzles is much too complicated for our purposes. For higher grade levels and curious minds you can recommend the article by Hannes Bassen, “Further Insight into the Mondrian Art Problem.”
Even since the Mondrian Problem was introduced, mathematicians have tried and continue to look for a general method that would give the solution for each case. You may want to watch Math Pickle’s video on “Mondrian Art Puzzles” where Gordon Hamilton demonstrates some of the complexity of these solutions.
Support and Extension
For students ready for additional extension in this lesson, consider asking to find the least possible number of colors that allows them to color their art so that no two same-colored squares/rectangles touch on an edge or vertex. (along with finding the lowest possible score)
Polypads for This Lesson
To assign these to your classes in Mathigon, save a copy to your Mathigon account. Click here to learn how to share Polypads with students and how to view their work.