FractaisIntrodução
Ao olhar a natureza, você deve ter notado plantas complexas como estas:


Esta samambaia consiste em muitas folhas pequenas que se ramificam em folhas maiores.


Este brócolis romanesco consiste em
Inicialmente, elas parecem formas altamente complexas - mas quando você olha mais de perto, pode perceber que as duas seguem um padrão relativamente simples: todas as partes individuais das plantas parecem exatamente iguais a toda planta, apenas menor. O mesmo padrão é repetido várias vezes, em escalas menores.
Em matemática, chamamos essa propriedade de auto-similaridade, e as formas que a possuem são chamadas de
Para criar nossos próprios fractais, temos que começar com um padrão simples e depois repeti-lo várias vezes, em escalas menores.
Um dos padrões mais simples pode ser um segmento de linha, com mais dois segmentos ramificados em uma extremidade. Se repetirmos esse padrão, os dois segmentos azuis também terão mais duas ramificações nas extremidades.
Você pode mover os pontos azuis para alterar o comprimento e o ângulo de todos os ramos. Aumente o número de iterações usando
Dependendo da posição dos galhos, é possível criar padrões completamente diferentes - parecendo a acima, uma ou . O que mais você pode encontrar?
Outro fractal famoso é o
Observe como a forma final é composta de três cópias idênticas de si mesma, e cada uma delas é composta de cópias ainda menores de todo o triângulo! Você pode continuar ampliando o triângulo para sempre, e os padrões e formas sempre continuarão se repetindo.
As plantas no começo deste capítulo parecem exatamente como fractais, mas é claramente impossível criar verdadeiros fractais na vida real. Se continuarmos repetindo o mesmo padrão repetidamente, cada vez menores, chegaremos a células, moléculas ou átomos que não podem mais ser divididos.
No entanto, usando a matemática, podemos pensar nas propriedades que os fractais reais “deveriam” ter - e são muito surpreendentes…
Dimensões do Fractal
Primeiro, vamos pensar na dimensão dos fractais. Uma linha tem dimensão
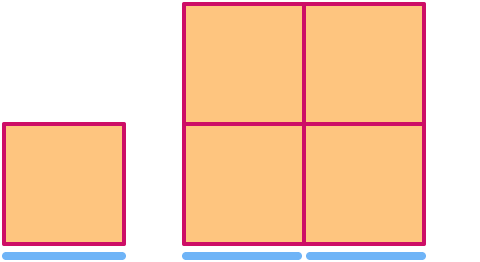
Um quadrado tem dimensão
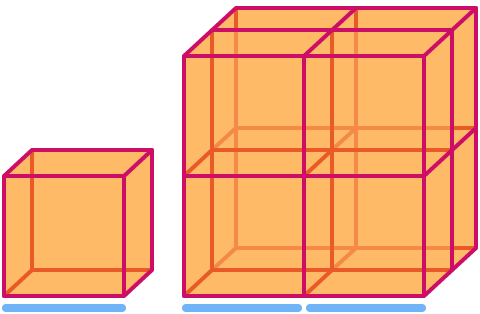
Um cubo tem dimensão
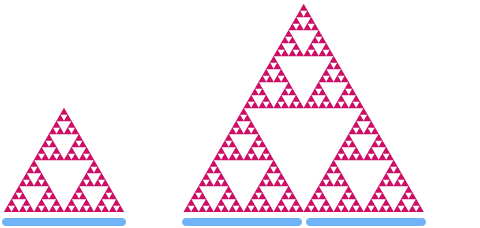
Agora vamos dar uma olhada no triângulo de Sierpinski. Se o ampliarmos por um fator de 2, você poderá ver que a "área" aumenta em um fator de
Digamos que d seja a dimensão do triângulo de Sierpinski. Usando o mesmo padrão acima, obtemos
Mas espere... como algo pode ter uma dimensão que não é um número inteiro? Parece impossível, mas esta é apenas uma das propriedades estranhas dos fractais. De fato, é isso que dá nome aos fractais: eles têm uma dimensão fracionária.
A cada iteração, removemos parte da área do triângulo de Sierpinski. Se pudéssemos fazer isso infinitamente várias vezes, não haveria realmente nenhuma área: é por isso que o triângulo de Sierpinski é algo entre uma área bidimensional e uma linha unidimensional.
Enquanto muitos fractais são auto-similares, uma definição melhor é que fractais são formas que possuem dimensão não inteira.
O floco de neve de Koch
Existem muitas formas na natureza que se parecem com fractais. Já vimos algumas plantas no início deste capítulo. Outros grandes exemplos são flocos de neve e cristais de gelo:
Para criar nosso próprio floco de neve fractal, precisamos encontrar novamente um procedimento simples que possamos aplicar repetidamente.
Como o triângulo de Sierpinski, vamos começar com um único triângulo equilátero. No entanto, em vez de remover triângulos menores a cada passo, adicionamos triângulos menores ao longo da aresta. O comprimento lateral de cada triângulo é
A forma resultante é chamada de
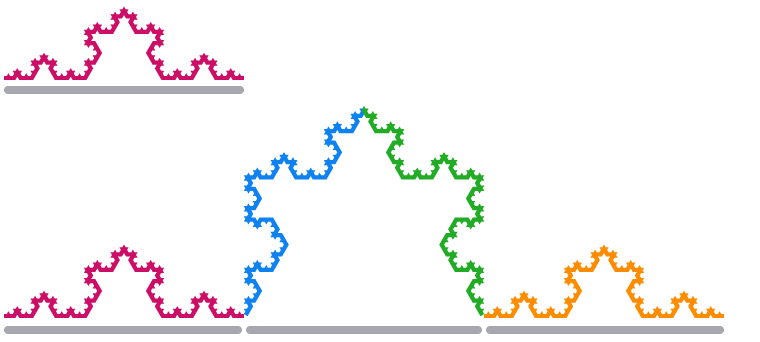
Quando ampliamos um segmento de borda do floco de neve de Koch por um fator 3, seu comprimento
Usando a mesma relação entre dimensões e fatores de escala como acima, obtemos a equação
Área_{span.check(when="blank-6")}_
Criar os flocos de neve de Koch é quase como uma




Após a primeira iteração, o número de novos triângulos adicionados aumenta em um fator de
Digamos que o
Usando a fórmula da soma de infinitos termos de uma
Perímetro
Também podemos tentar calcular o perímetro do floco de neve de Koch. Como já vimos antes, o comprimento do perímetro muda em um fator de
Isso significa que, mais uma vez, temos uma série geométrica - mas, neste caso,

Se isso parecer contra-intuitivo, lembre-se de que multiplicamos o perímetro por
É quase impensável que você possa ter uma forma com uma área finita e também um perímetro infinito - mas essa é apenas uma das muitas propriedades inesperadas dos fractais.
Você pode encontrar outras maneiras de criar seus próprios fractais?
"Minha alma está espiralando em fractais congelados por toda parte ..."
Esponja de Menger
Os fractais não precisam ser "planos", como muitos dos exemplos acima. Um dos fractais mais famosos que parecem tridimensionais é a esponja de Menger, nomeada em homenagem ao matemático
Começamos com um cubo sólido e fazemos repetidamente furos cada vez menores em seus lados. Toda nova iteração de furos possui
Um cubo
Agora, podemos tentar calcular a dimensão d da esponja de Menger, exatamente como fizemos no floco de neve de Koch acima. Nesse caso, obtemos
Se você imaginar cortar cada vez mais furos, infinitas vezes, não haveria volume real. É por isso que o cubo de Menger "não é bem" tridimensional!
Litoral do Fractal
Uma das principais características de todos os fractais que vimos até agora é que você pode "aumentar o zoom" para sempre e sempre encontrar novos padrões. Por volta de 1920, o matemático britânico
Você começa com a forma básica do país e, à medida que aumenta o zoom, adiciona enseadas de rios, baías e estuários, depois penhascos, rochas, seixos e assim por diante:
Esse é um problema significativo ao tentar calcular o comprimento da fronteira de um país - como você decide a que distância deve aumentar o zoom e quais cantos e recantos devem ser incluídos?
Uma maneira de medir o comprimento da costa da Grã-Bretanha, por exemplo, é pegar uma régua longa, caminhar ao redor de suas praias e somar todas as distâncias.
Se a régua tem
Poderíamos continuar, com réguas cada vez menores, e cada vez nosso resultado para a extensão da costa iria ficar um pouco mais longo. Assim como o floco de neve de Koch, parece que a costa da Grã-Bretanha é infinitamente longa! Isso costuma ser chamado de paradoxo do litoral.
Algumas décadas depois, enquanto trabalhava na IBM, o matemático Benoit Mandelbrot encontrou o trabalho de Richardson em um livro descartado da biblioteca. Ele reconheceu seu significado e também como ele se relacionava com pesquisas mais recentes sobre fractais e dimensões.
O litoral da Grã-Bretanha certamente "parece" fractal, mas não é auto-semelhante, como outros fractais que já vimos antes. Para encontrar seu tamanho, podemos desenhá-lo em uma grade e contar o número de células com as quais ele se cruza.
Inicialmente, existem 88 células que se cruzam. Se ampliarmos a costa por um fator de 2, haverá 197 células que se cruzam - mais que o dobro!
O tamanho da costa aumentou em um fator de
Se repetirmos isso com grades maiores, descobriremos que a dimensão da costa da Grã-Bretanha é de aproximadamente 1,21. Mandelbrot percebeu que essa dimensão fractal também é uma medida da rugosidade de uma forma - um novo conceito, para o qual ele encontrou aplicações importantes em muitas outras áreas da matemática e da ciência.
Mais fractais na natureza e na tecnologia
Embora os fractais verdadeiros nunca possam aparecer na natureza, há muitos objetos que quase se parecem com fractais. Já vimos plantas, flocos de neve e costas, e aqui estão mais alguns exemplos:
Cordilheira na Ásia Central
Delta do rio Ganges na Índia
Raios
Vasos sanguíneos na retina
Grand Canyon nos EUA
Nuvens
Todos esses objetos podem parecer completamente aleatórios, mas, assim como os fractais, existe um padrão subjacente que determina como eles são formados. A matemática pode nos ajudar a entender melhor as formas, e os fractais têm aplicações em áreas como medicina, biologia, geologia e meteorologia.
Terreno fractal gerado por computador
Também podemos usar fractais para criar "cópias" realistas da natureza, por exemplo, como paisagens e texturas usadas em videogames ou filmes gerados por computador. A água, montanhas e nuvens nesta imagem são feitas inteiramente por um computador, com a ajuda de fractais!
E podemos até reverter esse processo para compactar imagens digitais e reduzir o tamanho do arquivo. Os primeiros algoritmos foram desenvolvidos por Michael Barnsley e Alan Sloan na década de 1980, e novos algoritmos ainda estão sendo pesquisados até hoje.