FractaisO Conjunto de Mandelbrot

Todos os fractais que vimos nos capítulos anteriores foram criados usando um processo de iteração: você começa com um padrão específico e depois o repete repetidamente.

Isso é semelhante a outro conceito em matemática que você viu antes: nas sequências recursivas você começa com um número específico e aplica nele repetidamente a mesma fórmula recursivamente para obter o próximo número da seqüência.

Vamos usar a fórmula recursiva xn=xn−12 como exemplo e plotar seus termos em uma linha numérica. Você pode alterar o valor de x0:

Observe como a sequência resultante pode se comportar de maneira muito diferente, dependendo do valor inicial x0:

Até agora, não aprendemos nada de novo. No entanto, cerca de um século atrás, os matemáticos começaram a explorar o que acontece com essas seqüências se você usar números complexos, em vez de usar apenas a reta dos números reais. Suas descobertas foram alguns dos resultados mais surpreendentes e bonitos de toda a matemática.

Conjuntos de Julia

Vamos usar a mesma sequência de antes, xn=xn−12, mas no plano complexo. Você pode mover a posição de x0, para ver o que acontece com os termos seguintes da sequência. Se a sequência parecer convergir, vamos colorir o ponto correspondente no plano em azul:

Como você pode ver, a sequência converge enquanto x0 estiver dentro do círculo unitáriofora do quadrado unitárioacima do eixo x (o círculo com raio 1, centralizado na origem).

Agora vamos tornar as coisas um pouco mais difíceis. Em vez de apenas elevar o quadrado do número anterior, também adicionamos a ele uma constante c (que pode ser qualquer número complexo). Em outras palavras, xn=xn−12+c. Você acha que ainda teremos um círculo de pontos convergentes? Que outras formas você acha que poderemos ver? Continuar

Neste diagrama, você pode mover a posição de x0 e alterar o valor de c:

As diferentes formas que são formadas pela coloração dos números são chamadas conjuntos de Julia. Eles foram descobertos independentemente por dois matemáticos franceses, Gaston Julia e Pierre Fatou, por volta de 1918.

Naquela época, não havia computadores para ajudar a visualizar como os conjuntos de Julia realmente eram. Matemáticos como Julia e Fatou foram capazes de raciocinar matematicamente sobre eles, mas eles só viram esboços rudes e desenhados à mão de como poderiam ser.

Hoje não temos esse problema. As imagens abaixo são de conjuntos diferentes de Julia. As cores diferentes indicam a rapidez com que a sequência nesse ponto diverge:

Continuar

O Conjunto de Mandelbrot

Ao criar os diferentes conjuntos de Julia, você deve ter notado que havia alguns valores de c para os quais cada sequência diverge, e todo o plano complexo permanece branco. Algumas décadas depois de Julia e Fatou, uma nova geração de matemáticos tentou mapear como eram essas áreas.

No exemplo anterior, escolhemos um valor fixo para c e, em seguida, alteramos a posição de x0 para colorir o plano. Agora, faremos o contrário: vamos fixar o valor em x0=0 e alterar o valor de c.

Mais uma vez, pinte o plano complexo para revelar a área na qual as seqüências permanecem limitadas. Quais formas você espera que apareçam?

xn=xn−12+${complex(c)}

x0=${complex(x0)}

x1=${complex(x1)}

x2=${complex(x2)}

x3=${complex(x3)}

…Limitada!Diverge!

Esse fractal é chamado de conjunto de Mandelbrot e, quando girado em 90 °, parece quase uma pessoa, com cabeça, corpo e dois braços. Foi definido e desenhado pela primeira vez em 1978, em um trabalho de pesquisa dos matemáticos Robert Brooks e Peter Matelski:

Alguns anos depois, Benoit Mandelbrot usou os poderosos computadores da IBM para criar uma visualização muito mais detalhada do fractal, que mais tarde recebeu o nome dele. As primeiras impressões pareciam diferentes do que ele esperava - até que ele percebeu que os técnicos que trabalhavam nas impressoras estavam limpando a “imprecisão” em torno da borda, assumindo que era causada por partículas de poeira ou erros da impressora, e não uma característica definidora de fractais ! Continuar

Como todos os fractais, podemos "ampliar" o conjunto de Mandelbrot para sempre, encontrando novos padrões em todas as escalas. Aqui você pode ampliar uma parte do conjunto de Mandelbrot chamado vale do cavalo-marinho. Pontos pretos estão dentro do conjunto de Mandelbrot, onde a sequência é limitada. Os pontos coloridos estão fora do conjunto de Mandelbrot, onde a sequência diverge e as cores diferentes indicam a rapidez com que a sequência cresce até o infinito:

Escala: ${pow(scale)}

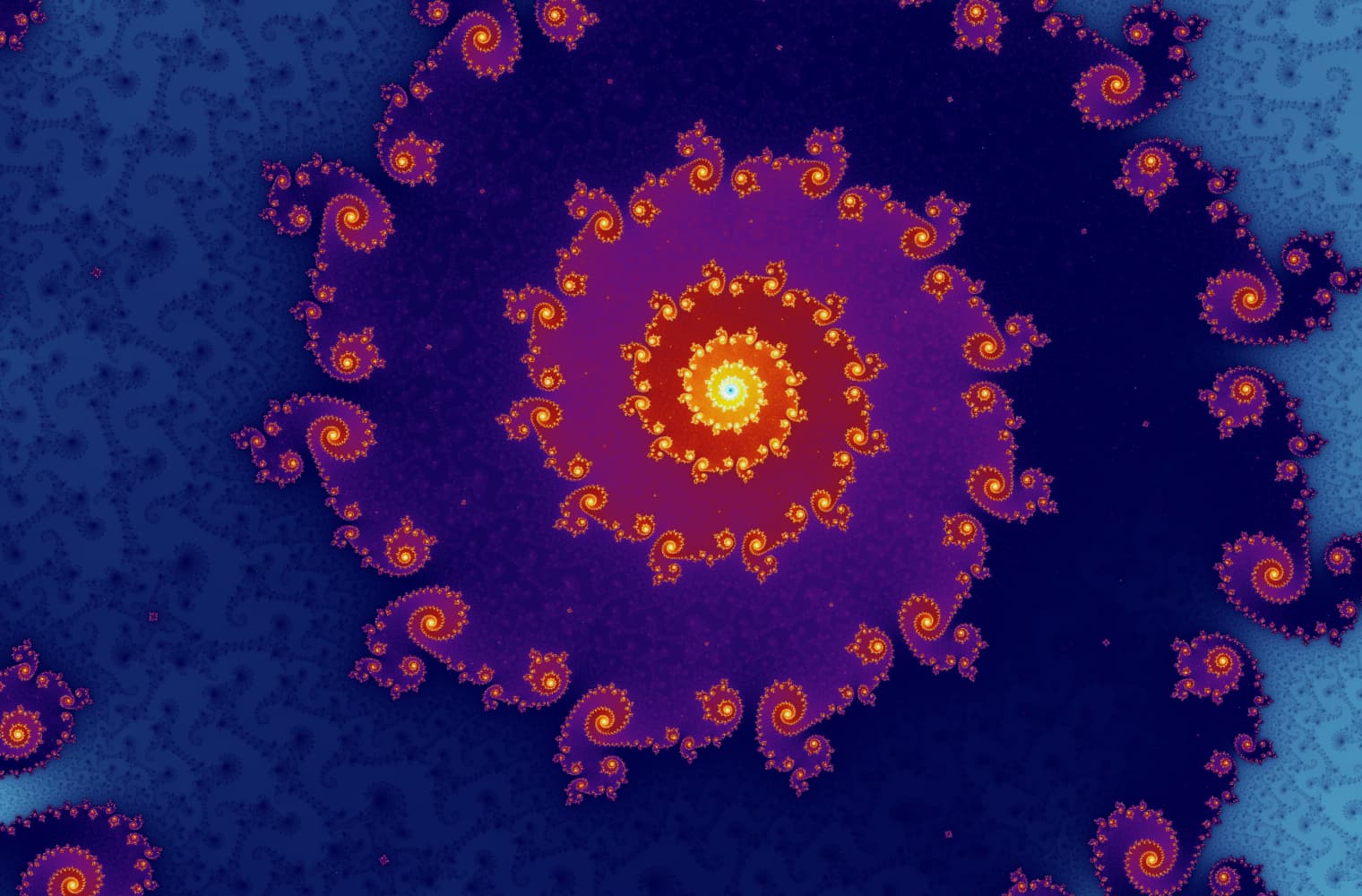
Esse controle deslizante consiste em 27 imagens individuais, até um nível de zoom acima de 14 quadrilhões ou 254. No total, eles levaram quase 45 minutos para renderizar em um laptop moderno. O conjunto de Mandelbrot pode ser criado com apenas uma equação única e simples, xn=xn−12+c, mas é infinitamente complexo e incrivelmente bonito.

Ao mover o valor de c ao redor do conjunto de Mandelbrot, você poderá notar uma propriedade curiosa:

• Todas as sequências no corpo principal [do conjunto Mandelbrot convergemdivergematingem uma órbita para um único ponto.
• As sequências dentro do bulbo grande no topo atingem uma órbitaconvergemdivergem consistindo em pontos.
• Sequências neste bulbo menor têm órbitas de período .

Todo bulbo tem uma órbita de tamanho diferente, com bulbos menores tendo cada vez mais pontos em suas órbitas. O tamanho dessas órbitas está intimamente relacionado ao mapa logístico, um conceito importante na teoria do caos.