Transformações e simetriaGrupos de Simetria e Papéis de Parede
Algumas formas têm mais de uma simetria - vamos dar uma olhada no








Você já mostrou acima que um quadrado tem
Também possui simetria rotacional em
E, finalmente, podemos pensar em "não fazer nada" como outro tipo especial de simetria - porque o resultado é (obviamente) o mesmo de antes. Isso às vezes é chamado de identidade .
No total, foram encontradas
Agora podemos começar a fazer aritmética com essas simetrias. Por exemplo, podemos adicionar duas simetrias para obter novas:






Sempre que você adiciona duas simetrias de um quadrado, obtém uma nova. Aqui está uma "calculadora de simetria", na qual você pode tentar:
Passe algum tempo brincando com a calculadora de simetria e tente encontrar padrões. Você pode completar essas observações?
- Adicionar duas rotações sempre dará
(ou a identidade). * Adicionar duas reflexões sempre dará (ou a identidade). * A adição das mesmas duas simetrias na ordem oposta resultado. * Adicionar a identidade .
Você já deve ter percebido que adicionar simetrias é realmente muito semelhante à adição inteiros :
- Adding two symmetries/integers always gives another symmetry/integer:
+ = 12 + 7 = 19 - Adding symmetries/integers is
associative :+ + = + + 4 + 2 + 5 = 4 + 2 + 5 - Every symmetry/integer has an inverse, another symmetry/integer which, when added, gives the identity:
+ = 4 + –4 = 0
Em matemática, qualquer coleção que possua essas propriedades é chamada de
Neste exemplo, começamos com as oito simetrias do quadrado. De fato, toda forma geométrica tem seu próprio grupo de simetria . Todos eles têm elementos diferentes, mas sempre satisfazem as três regras acima.
Grupos aparecem em todos os lugares na matemática. Os elementos podem ser números ou simetrias, mas também polinômios, permutações, matrizes, funções ... qualquer coisa que obedeça às três regras. A idéia principal da teoria dos grupos é que não estamos interessados nos elementos individuais, apenas em como eles interagem .
Por exemplo, os grupos de simetria de diferentes moléculas podem ajudar os cientistas a prever e explicar as propriedades dos materiais correspondentes.
Os grupos também podem ser usados para analisar a estratégia vencedora em jogos de tabuleiro, o comportamento dos vírus na medicina, diferentes harmonias na música e muitos outros conceitos ...
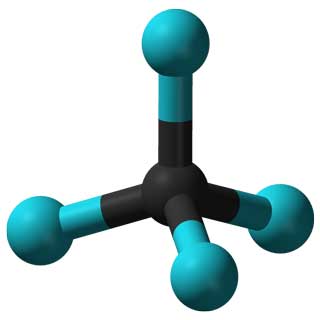
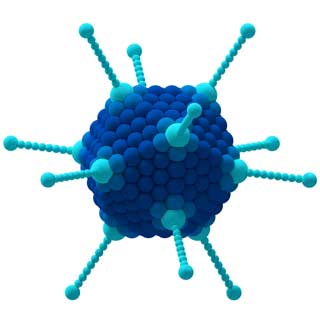
As propriedades da molécula CCl 4 (esquerda) e do adenovírus (direita) são determinadas por suas simetrias.
Grupos de papel de parede
Nas seções anteriores , vimos dois tipos diferentes de simetria, correspondentes a duas transformações diferentes: rotações e reflexões. Mas há também uma simetria para o terceiro tipo de transformação rígida:


Honyecomb hexagonal


Revestimento de parede em cerâmica
Além da simetria reflexiva, rotacional e translacional, existe ainda um quarto tipo:


Um padrão pode ter mais de um tipo de simetria. E, assim como nos quadrados, podemos encontrar o
Esses grupos não informam muito sobre a aparência do padrão (por exemplo, suas cores e formas), exatamente como é repetido . Vários padrões diferentes podem ter o mesmo grupo de simetria - desde que sejam organizados e repetidos da mesma maneira.


Esses dois padrões têm as mesmas simetrias, embora pareçam muito diferentes. Mas simetrias não são sobre cores ou formas superficiais.


Esses dois padrões também têm as mesmas simetrias - embora pareçam mais semelhantes aos padrões correspondentes à esquerda do que um ao outro.
Acontece que, embora existam infinitos padrões possíveis, todos eles têm um de apenas 17 grupos de simetria diferentes. Estes são chamados de Grupos de Papéis de Parede . Cada grupo de papel de parede é definido por uma combinação de translações, rotações, reflexões e reflexões planas. Você pode ver os

Group 1 – P1
Only translations div img(src="/content/transformations/images/wallpapers/p2.svg" width=360, height=240) p.caption Group 2 – P2 Rotations of order 2, translations div img(src="/content/transformations/images/wallpapers/p3.svg" width=360, height=240) p.caption Group 3 – P3 Rotations of order 3 (120°), translations div img(src="/content/transformations/images/wallpapers/p4.svg" width=360, height=240) p.caption Group 4 – P4 Four rotations of order 2 (180°), translations div img(src="/content/transformations/images/wallpapers/p6.svg" width=360, height=240) p.caption Group 5 – P6 Rotations of order 2, 3 and 6 (60°), translations div img(src="/content/transformations/images/wallpapers/pm.svg" width=360, height=240) p.caption Group 6 – PM Parallel axes of reflection, translations div img(src="/content/transformations/images/wallpapers/pmm.svg" width=360, height=240) p.caption Group 7 – PMM Perpendicular reflections, rotations of order 2, translations div img(src="/content/transformations/images/wallpapers/p4m.svg" width=360, height=240) p.caption Group 8 – P4M Rotations (ord 2 + 4), reflections, glide reflections, translations div img(src="/content/transformations/images/wallpapers/p6m.svg" width=360, height=240) p.caption Group 9 – P6M Rotations (ord 2 + 6), reflections, glide reflections, translations div img(src="/content/transformations/images/wallpapers/p3m1.svg" width=360, height=240) p.caption Group 10 – P3M1 Rotations of order 3, reflections, glide reflections, translations div img(src="/content/transformations/images/wallpapers/p31m.svg" width=360, height=240) p.caption Group 11 – P31M Rotations of order 3, reflections, glide reflections, translations div img(src="/content/transformations/images/wallpapers/p4g.svg" width=360, height=240) p.caption Group 12 – P4G Rotations (ord 2 + 4), reflections, glide reflections, translations div img(src="/content/transformations/images/wallpapers/cmm.svg" width=360, height=240) p.caption Group 13 – CMM Perpendicular reflections, rotations of order 2, translations div img(src="/content/transformations/images/wallpapers/pmg.svg" width=360, height=240) p.caption Group 14 – PMG Reflections, glide reflections, rotations of order 2, translations div img(src="/content/transformations/images/wallpapers/pg.svg" width=360, height=240) p.caption Group 15 – PG Parallel glide reflections, translations div img(src="/content/transformations/images/wallpapers/cm.svg" width=360, height=240) p.caption Group 16 – CM Reflections, glide reflections, translations div img(src="/content/transformations/images/wallpapers/pgg.svg" width=360, height=240) p.caption Group 17 – PGG Perpendicular glide reflections, rotations of order 2, translations
Infelizmente, não há uma razão simples para haver 17 desses grupos, e provar que isso requer matemática mais avançada. Em vez disso, você pode tentar desenhar seus próprios padrões repetidos para cada um dos 17 grupos de papéis de parede:
Examples of other students’ drawings



Os grupos de papéis de parede eram sobre padrões planos e bidimensionais. Podemos fazer algo semelhante para padrões tridimensionais: eles são chamados de grupos cristalográficos e existem 219 deles!
Além de translações, reflexões, rotações e reflexões de deslizamento, esses grupos incluem simetrias como planos de deslizamento e eixos de parafuso (pense no movimento ao desaparafusar uma garrafa).
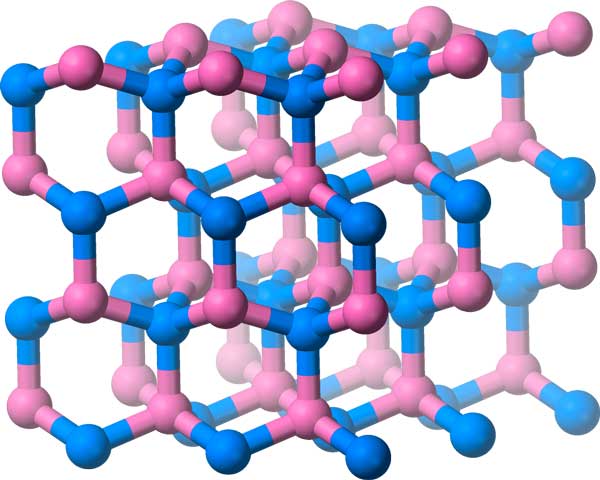
O nitreto de boro tem suas moléculas dispostas nessa estrutura cristalina, que possui um grupo de simetria tridimensional.