Polígonos e PoliedrosPavimentações

Polígonos aparecem em toda parte na natureza. Eles são especialmente úteis se você deseja agrupar uma área grande, porque é possível encaixar polígonos sem espaços ou sobreposições. Padrões como esse são chamados de mosaicos .

Favo de mel

Pele de cobra de leite de Sinaloan

Estrutura celular das folhas

Colunas de basalto na calçada do gigante na Irlanda do Norte

Pele de abacaxi

Concha de uma tartaruga

Os seres humanos copiaram muitos desses padrões naturais em arte, arquitetura e tecnologia - da Roma antiga até o presente. Aqui estão alguns exemplos:

Padrão de pavimento

Estufa no Eden Project na Inglaterra

Mosaico em Alhambra

Telhado no Museu Britânico em Londres

Pavilhão de mosaico celular em Sydney

Estudo da Divisão Regular do Avião com Répteis , MC Escher

Aqui você pode criar seus próprios mosaicos usando polígonos regulares. Simplesmente arraste novas formas da barra lateral para a tela. Quais as formas de mosaico bem? Existe alguma forma que não exagere? Tente criar padrões interessantes!

Examples of other students’ tessellations

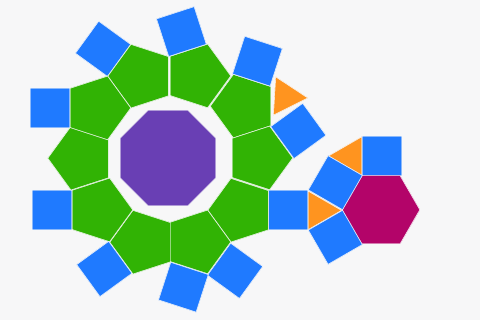
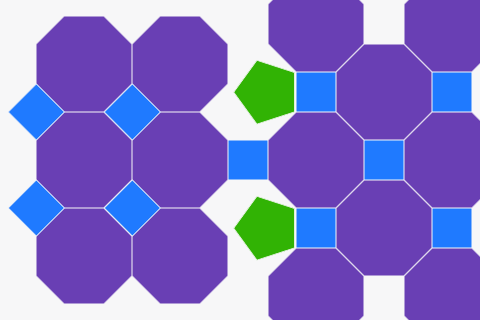
Pavimentações de polígonos regulares

Você deve ter notado que alguns polígonos regulares (como ) pavimentam muito facilmente, enquanto outros (como ) não parecem ter um mosaico.

Isso tem a ver com o tamanho de seus ângulos internos , que aprendemos a calcular antes. Em todos os vértices do mosaico, os ângulos internos de vários polígonos diferentes se encontram. Precisamos de todos esses ângulos para somar °, caso contrário, haverá uma lacuna ou uma sobreposição.

Triângulos em porque 6 × 60° = 360°.

Quadrados em porque 4 × 90° = 360°.

Pentágonos porque múltiplos de 108° não somam 360°.

Hexágonos em porque 3 × 120° = 360°.

Da mesma forma, você pode verificar se, assim como os pentágonos, qualquer polígono regular com 7 ou mais lados não é um mosaico. Isso significa que os únicos polígonos regulares que são mosaicos são triângulos, quadrados e hexágonos!

É claro que você pode combinar diferentes tipos de polígonos regulares em um mosaico, desde que seus ângulos internos possam somar 360°:

Squares and triangles
90° + 90° + 60° + 60° + 60° = 360°

Hexagons and triangles
120° + 120° + 60° + 60° = 360°

Hexagons and triangles
120° + 60° + 60° + 60° + 60° = 360°

Hexagons, squares and triangles
120° + 90° + 90° + 60° = 360°

Octagons and squares
135° + 135° + 90° = 360°

Dodecagons (12-gons) and triangles
150° + 150° + 60° = 360°

Dodecagons, hexagons and squares
150° + 120° + 90° = 360°

Pavimentações de polígonos irregulares

Também podemos tentar fazer mosaicos com polígonos irregulares - desde que tenhamos cuidado ao girá-los e organizá-los.

Acontece que você pode mosaico não apenas triângulos equilaterais, mas qualquer triângulo ! Tente mover os vértices neste diagrama.

A soma dos ângulos internos de um triângulo é de °. Se usarmos cada ângulo em cada vértice do mosaico, obtemos 360°:

Surpreendentemente, qualquer quadrilátero também pavimenta! A soma dos ângulos internos é de °, portanto, se usarmos cada ângulo em cada vértice do mosaico, obtemos 360°.

Pentágonos são um pouco mais complicados. Já vimos que pentágonos regulares , mas e os não-regulares?

Aqui estão três exemplos diferentes de pavimentações com pentágonos. Eles não são regulares , mas são polígonos de 5 lados perfeitamente válidos.

Até agora, os matemáticos encontraram apenas 15 tipos diferentes de mosaicos com pentágonos (convexos) - o mais recente foi descoberto em 2015. Ninguém sabe se existem outros ou se esses 15 são os únicos…

Pavimentações em Arte

Os mosaicos são uma ferramenta e inspiração para muitos artistas, arquitetos e designers - o mais famoso é o artista holandês MC Escher . O trabalho de Escher contém criaturas, padrões e paisagens estranhas e mutantes:

“Sky and Water I” (1938)

“Lizard” (1942)

“Lizard, Fish, Bat” (1952)

“Butterfly” (1948)

“Two Fish” (1942)

“Shells and Starfish” (1941)

Essas obras de arte geralmente parecem divertidas e sem esforço, mas os princípios matemáticos subjacentes são os mesmos de antes: ângulos, rotações, traduções e polígonos. Se a matemática não estiver certa, o mosaico não vai funcionar!

“Metamorphosis II” by M. C. Escher (1940)

Penrose Tilings

Todos os mosaicos que vimos até agora têm uma coisa em comum: são periódicos . Isso significa que eles consistem em um padrão regular que é repetido várias vezes. Eles podem continuar para sempre em todas as direções e terão a mesma aparência em todos os lugares.

Na década de 1970, o matemático e físico britânico Roger Penrose descobriu mosaicos não periódicos - eles ainda continuam infinitamente em todas as direções, mas nunca parecem exatamente iguais. Eles são chamados de inclinações de Penrose e você só precisa de alguns tipos diferentes de polígonos para criar um:

Move the slider to reveal the underlying structure of this tessellation. Notice how you have the same patterns at various scales: the small yellow pentagons, blue stars, orange rhombi and green ‘ships’ appear in their original size, in a slightly larger size and an even larger size. This self-similarity can be used to prove that this Penrose tiling is non-periodic.

Penrose estava explorando mosaicos apenas por diversão, mas acontece que a estrutura interna de alguns materiais reais (como o alumínio) segue um padrão semelhante. O padrão foi usado até em papel higiênico, porque os fabricantes perceberam que um padrão não periódico pode ser enrolado sem protuberâncias.

Mudar idioma

Entrar no Mathigon

Compartilhar

Redefinir progresso