Polígonos e PoliedrosSólidos platônicos

No início deste curso, definimos polígonos regulares como polígonos particularmente "simétricos", onde todos os lados e ângulos são iguais. Podemos fazer algo semelhante para o poliedro.

Em um poliedro regular, todas as faces são do mesmo tipo de polígono regular e o mesmo número de faces se encontra em todos os vértices . Os poliedros com essas duas propriedades são chamados sólidos platônicos , nomeados em homenagem ao filósofo grego Platão .

Então, como são os sólidos platônicos - e quantos deles existem? Para criar uma forma tridimensional, precisamos de pelo menos faces para se encontrar em cada vértice. Vamos começar sistematicamente com o menor polígono regular: triângulos equilaterais:

E sete ou mais triângulos em todos os vértices também não produzem novos poliedros: não há espaço suficiente ao redor de um vértice, para caber em tantos triângulos.

Isso significa que encontramos sólidos platônicos compostos por triângulos. Vamos para o próximo polígono regular: quadrados.

Em seguida, vamos tentar pentágonos regulares:

Se pentágonos se encontram em cada vértice, obtemos o dodecaedro . Tem faces. ("Dodeca" significa "doze" em grego.)

O próximo polígono regular a ser experimentado são hexágonos:

Se três hexágonos se encontram em cada vértice, obtemos imediatamente um mosaico poliedro hexaedro . Como não há espaço para mais de três, parece que não há sólidos platônicos constituídos por hexágonos.

O mesmo acontece com todos os polígonos regulares com mais de seis lados. Eles não pavimentam, e certamente não temos polígonos tridimensionais.

Isso significa que existem apenas sólidos platônicos! Vamos dar uma olhada em todos eles juntos:

Observe como o número de faces e vértices é trocado o mesmo para cubo e octaedro , assim como dodecaedro e icosaedro , enquanto o número de arestas permanece o mesmo são diferentes . Esses pares de sólidos platônicos são chamados de sólidos duplos .

Podemos transformar um poliedro em seu dual, substituindo cada face por um vértice e cada vértice por uma face. Essas animações mostram como:

O tetraedro é duplo consigo mesmo. Como possui o mesmo número de faces e vértices, trocá-los não mudaria nada.

Platão acreditava que toda a matéria do Universo consiste em quatro elementos: Ar, Terra, Água e Fogo. Ele achava que todo elemento correspondia a um dos sólidos platônicos, enquanto o quinto representaria o universo como um todo. Hoje sabemos que existem mais de 100 elementos diferentes que consistem em átomos esféricos, e não em poliedros.

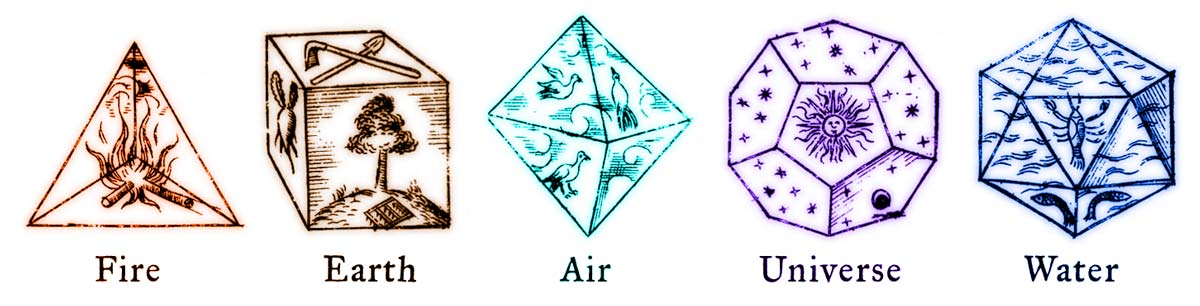
Images from Johannes Kepler’s book “Harmonices Mundi” (1619)

Sólidos Arquimedeanos

Os sólidos platônicos são poliedros particularmente importantes, mas existem inúmeros outros.

Os sólidos arquimedianos , por exemplo, ainda precisam ser compostos de polígonos regulares , mas você pode usar vários tipos diferentes. Eles têm o nome de outro matemático grego, Arquimedes de Siracusa , e há 13 deles:

Formulários

Platão estava errado ao acreditar que todos os elementos consistiam em sólidos platônicos. Mas os poliedros comuns têm muitas propriedades especiais que os fazem aparecer em outros lugares da natureza - e podemos copiar essas propriedades na ciência e na engenharia.