Sequências e padrõesSequências Aritméticas e Geométricas

Em 1682, o astrônomo Edmond Halley observou um fenômeno incomum: um objeto branco brilhante com uma cauda longa que se movia pelo céu noturno. Era um cometa __>>>>, uma rocha pequena e gelada que voava pelo espaço, deixando para trás um rastro de poeira e gelo.

Halley lembrou que outros astrônomos haviam observado cometas semelhantes muito antes: um em 1530 e outro em 1606. Observe que a diferença entre duas observações consecutivas é a mesma nos dois casos: anos.

Image of Halley’s Comet,
taken in 1986 on Easter Island

Halley concluiu que todas as três observações eram de fato do mesmo cometa - que agora é chamado de cometa de Halley. Está orbitando em torno do sol e passa pela Terra aproximadamente a cada 76 anos. Ele também previu quando o cometa seria visível a seguir:

1530, 1606*{span.arrow}+76*, 1682*{span.arrow}+76*, 1758*{span.arrow}+76*, +76, +76, +76, …

Na verdade, o intervalo de tempo nem sempre é exatamente 76 anos: pode variar em um ou dois anos, pois a órbita do cometa é interrompida por outros planetas. Hoje sabemos que o cometa de Halley foi observado pelos astrônomos antigos em 240 aC!

Depections of Halley’s comet throughout time: a Babylonian tablet (164 BC), a medival tapestry (1070s), a science magazine (1910) and a Soviet stamp (1986).

Um grupo diferente de cientistas está investigando o comportamento de uma bola de tênis quicando. Eles largaram a bola a uma altura de 10 metros e mediram sua posição ao longo do tempo. A cada salto, a bola perde parte da sua altura original:

Os cientistas notaram que a bola perde 20% de sua altura após cada salto. Em outras palavras, a altura máxima de cada salto é 80% da altura anterior. Isso permitiu prever a altura de cada salto seguinte:

10, 8*{span.arrow}×0.8*, ×0.8, ×0.8, 4.096*{span.arrow}×0.8*, 3.277*{span.arrow}×0.8*, 2.621*{span.arrow}×0.8*, 2.097*{span.arrow}×0.8*, …

Definições

Se você comparar esses dois problemas, poderá notar que existem muitas semelhanças: a sequência do cometa de Halley tem a mesma diferença entre termos consecutivos, enquanto a sequência de bolas de tênis bate na mesma proporção [[619} entre termos consecutivos.

Sequências com essas propriedades têm um nome especial:

Uma sequência aritmética tem uma constante de diferença d entre termos consecutivos.

O mesmo número é adicionado ou subtraído a cada termo, para produzir o próximo.

Uma sequência geométrica possui uma razão constante r entre termos consecutivos.

Cada termo é multiplicado ou dividido pelo mesmo número, para produzir o próximo.

Aqui estão algumas sequências diferentes. Você pode determinar quais são aritméticos, geométricos ou nenhum, e quais são os valores de d e r?

2, 4, 8, 16, 32, 64,…

é , com razão .

2, 5, 8, 11, 14, 17,…

é , com diferença .

17, 13, 9, 5, 1, –3,…

é , com diferença .

2, 4, 7, 11, 16, 22,…

não .

40, 20, 10, 5, 2,5, 1,25,…

é , com razão .

Para definir uma seqüência aritmética ou geométrica, precisamos saber não apenas a diferença ou razão comum, mas também o valor inicial (chamado a). Aqui você pode gerar suas próprias seqüências e plotar seus valores em um gráfico, alterando os valores de a, d e r. Você consegue encontrar algum padrão?

Sequência Aritmética #### {.m-red}

a = ${a}, d = ${d}

${arithmetic(a,d,0)}, ${arithmetic(a,d,1)}, ${arithmetic(a,d,2)}, ${arithmetic(a,d,3)}, ${arithmetic(a,d,4)}, ${arithmetic(a,d,5)}, …

Sequência geométrica

a = ${b}, r = ${r}

${geometric(b,r,0)}, ${geometric(b,r,1)}, ${geometric(b,r,2)}, ${geometric(b,r,3)}, ${geometric(b,r,4)}, ${geometric(b,r,5)}, …

Observe como todas as seqüências aritméticas parecem muito semelhantes: se a diferença é positiva, elas constantemente, e se a diferença é negativa, elas .

Seqüências geométricas, por outro lado, podem se comportar de maneira completamente diferente com base nos valores de a e r:

Se , os termos , até o infinito. Os matemáticos dizem que a sequência diverge.

Se , os termos sempre . Dizemos que a sequência converge.

Se , os termos alternarão entre positivo e negativo, enquanto o seu aumenta.

Você aprenderá mais sobre convergência e divergência na última seção deste curso.

Fórmulas Recursivas e Explícitas

Na seção anterior, você aprendeu que uma fórmula recursiva informa o valor de cada termo como uma função dos termos anteriores. Aqui estão as fórmulas recursivas para sequências aritméticas e geométricas:

xn=

Um problema com as fórmulas recursivas é que, para encontrar o 100º termo, por exemplo, primeiro precisamos calcular os 99 termos anteriores - e isso pode levar muito tempo. Em vez disso, podemos tentar encontrar uma fórmula explícita, que nos informa o valor do termo n diretamente.

Para sequências aritméticas, temos que adicionar d a cada passo:

x1= a

x2= a+d

x3= a+d+d

x4=

x5=

No termo n, estamos adicionando cópias de d, de modo que a fórmula geral é

xn=a+d×n−1.

Para sequências geométricas, temos que multiplicar r a cada passo:

x1=a

x2=a×r

x3=a×r×r

x4=

x5=

No termo n, multiplicamos cópias de r, de modo que a fórmula geral é

xn=a×rn−1.

Aqui está um resumo de todas as definições e fórmulas que você viu até agora:

Uma sequência aritmética possui primeiro termo a e diferença comum d entre termos consecutivos.

Fórmula recursiva: xn=xn−1+d

Fórmula explícita: xn=a+d×n−1

Uma sequência geométrica tem primeiro termo a e razão comum r entre termos consecutivos.

Fórmula recursiva: xn=xn−1×r

Fórmula explícita: xn=a×rn−1

Agora, vamos dar uma olhada em alguns exemplos em que podemos usar tudo isso!

Pague adiante

Aqui está um pequeno clipe do filme Pay it Forward, onde Trevor, de 12 anos, explica sua idéia de tornar o mundo um lugar melhor:

A essência da ideia de Trevor é que, se todos "pagarem adiante", uma única pessoa poderá ter um enorme impacto no mundo:

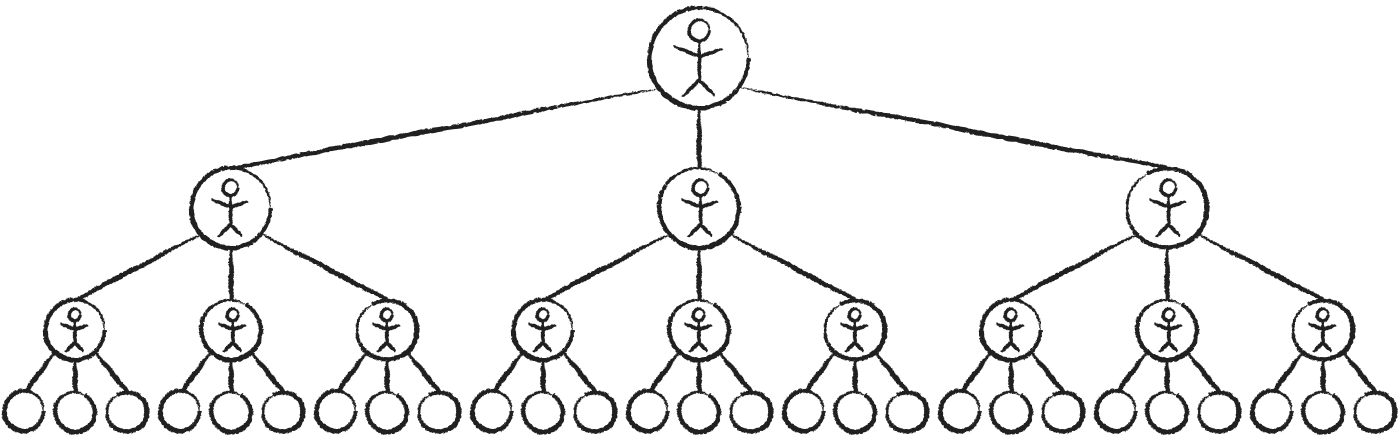
Observe como o número de pessoas em cada etapa forma uma , com razão comum :

1, 3*{span.arrow}×3*, 9*{span.arrow}×3*, ×3, ×3, ×3, …

Usando a fórmula explícita para seqüências geométricas, podemos calcular quantas novas pessoas são afetadas a qualquer etapa:

xn =

O número de pessoas aumenta incrivelmente rapidamente. Na 10ª etapa, você alcançaria 19.683 novos e, após 22 etapas, alcançaria mais pessoas do que as que atualmente estão vivas na Terra.

Essa sequência de números tem um nome especial: os poderes de de 3. Como você pode ver, todo termo é na verdade apenas um poder diferente de de 3:

30, 31, 32, 33, 34, 35, …

Quem quer ser um milionário?

EM BREVE!

O problema do tabuleiro de xadrez

EM BREVE!

Mudar idioma

Entrar no Mathigon

Compartilhar

Redefinir progresso