Sequências e padrõesNúmeros de Fibonacci
Imagine que você recebeu um par de coelhos bebê, um macho e uma fêmea. São coelhos muito especiais, porque nunca morrem, e a fêmea dá à luz um novo par de coelhos exatamente uma vez por mês (sempre outro par de machos e fêmeas).




















No mês seguinte, você teria 13 pares de coelhos: os 8 do mês anterior, mais 5 novos conjuntos de bebês. Você pode detectar um padrão nesta sequência?
O número de coelhos em um determinado mês é
Você pode calcular o número de coelhos depois de mais alguns meses?
1, 1, 2, 3, 5, 8,
Então, após 12 meses, você terá 144 pares de coelhos!
Essa sequência de números é chamada de
Quando Fibonacci nasceu em 1175, a maioria das pessoas na Europa ainda usava o
Quando ele retornou à Itália, Fibonacci escreveu um livro chamado Liber Abaci (latim para "O Livro de Cálculos"), onde ele introduziu os novos algarismos arábicos pela primeira vez nos comerciantes europeus. Eles foram um sucesso imediato - e ainda os usamos hoje.
Em uma das páginas de seu livro, ele também investigou os padrões de criação de coelhos - é por isso que os números de Fibonacci foram nomeados em homenagem a ele.
Pages from Fibonacci’s Liber Abaci
Certamente, os números de Fibonacci não são como os coelhos realmente povoam na vida real. Os coelhos não têm exatamente um filho masculino e uma fêmea todos os meses, e não consideramos os coelhos que morrem eventualmente.
Mas acontece que existem muitos outros lugares na natureza onde os números de Fibonacci aparecem: por exemplo, as espirais nas plantas. Você pode contar quantas espirais existem em cada direção?
Esta pinha possui
Este girassol possui 34 espirais no sentido horário e 55 espirais no sentido anti-horário.
Nos dois casos, os números de espirais são números consecutivos de Fibonacci. O mesmo vale para muitas outras plantas: na próxima vez que sair, conte o número de pétalas em uma flor ou o número de folhas em um caule. Muitas vezes você descobrirá que são números de Fibonacci!
Claro, isso não é apenas uma coincidência. Há uma razão importante pela qual a natureza gosta da sequência de Fibonacci, sobre a qual você aprenderá mais tarde.
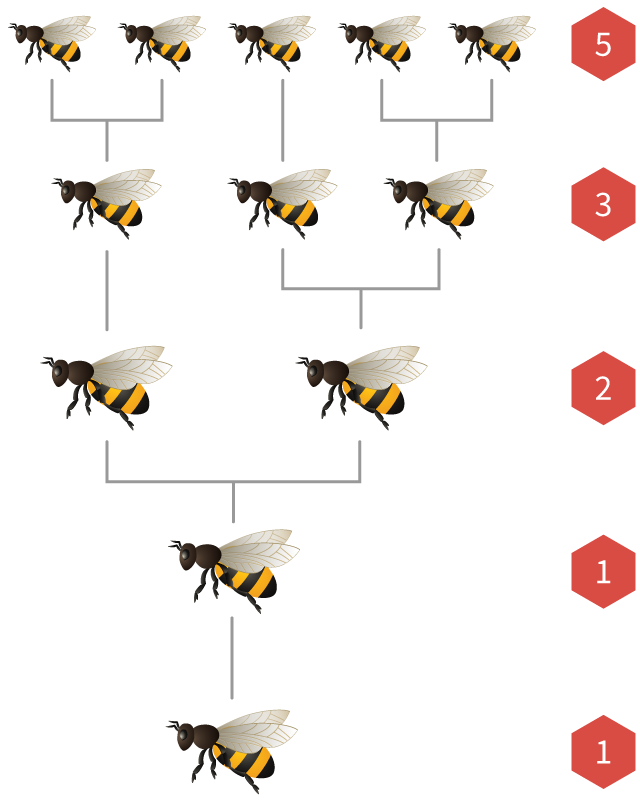
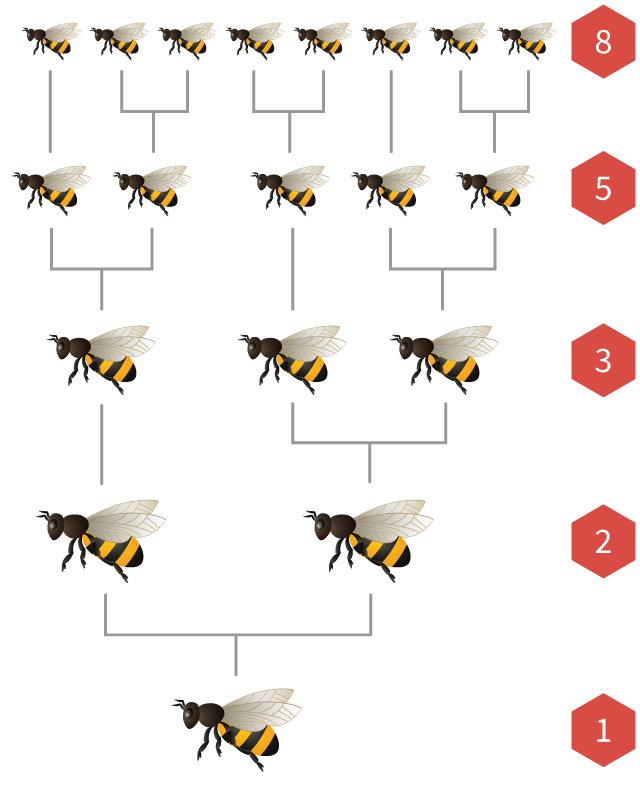
Os números de Fibonacci também aparecem nas populações de abelhas.
Em toda colônia de abelhas há uma única rainha que coloca muitos ovos. Se um ovo é fertilizado por uma abelha macho, ele choca em uma abelha fêmea. Se não for fertilizado, chocará-se em uma abelha macho (chamada drone).
Isso significa que as abelhas têm
Se desenharmos a árvore ancestral de uma abelha, o número de pais, avós, bisavós e gerações anteriores são sempre números de Fibonacci!
Ocasionalmente, jovens abelhas são alimentadas com alimentos especiais chamados “geléia real”. Nesse caso, eles se transformam em rainhas e voam para iniciar uma nova colméia.
A proporção áurea
Assim como os números quadrados
A cada passo, os quadrados formam um retângulo maior. Sua largura e altura são sempre dois números consecutivos de Fibonacci. A proporção de aspecto do retângulo é a proporção de sua largura e altura:
Observe como, à medida que adicionamos mais e mais quadrados, a proporção parece se aproximar cada vez mais de um número específico em torno de 1,6. Esse número é chamado de
Muitas pessoas acreditam que a proporção áurea é particularmente esteticamente agradável. É por isso que é frequentemente usado por artistas e arquitetos - como nesses dois exemplos:

Diz-se que o escultor grego Phidias usou a proporção áurea ao projetar o Parthenon em Atenas. A primeira letra de seu nome,

O Sacramento da Última Ceia, do artista espanhol Salvador Dalí, é uma das muitas pinturas na proporção áurea. No fundo, você também pode ver um grande
Podemos aproximar a proporção áurea dividindo [[dois números consecutivos de Fibonacci.
No entanto, verifica-se que o valor exato de
Espirais de Fibonacci
A proporção áurea explica por que os números de Fibonacci aparecem na natureza, como o girassol e a pinha que você viu no início desta seção.
Ambas as plantas crescem para fora do centro (uma parte da planta chamada meristema). À medida que novas sementes, folhas ou pétalas são adicionadas, elas empurram as existentes ainda mais para fora.
Mova o controle deslizante à direita para visualizar como uma planta cresce. Observe como cada folha é adicionada em uma rotação diferente da anterior. O ângulo entre duas folhas consecutivas é sempre o mesmo.
É importante que as flores escolham um ângulo adequado: as folhas ou sementes devem ser aproximadamente igualmente espaçadas para que obtenham a maior quantidade de luz solar e nutrientes. No diagrama abaixo, você pode explorar a aparência de um girassol com ângulos diferentes entre suas sementes:
Você deve se lembrar de cima, que as proporções de números consecutivos de Fibonacci se aproximam cada vez mais da proporção áurea - e é por isso que, se você contar o número de espirais em uma planta, geralmente encontrará um número de Fibonacci.
É importante lembrar que a natureza não sabe sobre os números de Fibonacci. A natureza também não consegue resolver equações para calcular a proporção áurea - mas, ao longo de milhões de anos, as plantas tiveram tempo de sobra para experimentar ângulos diferentes e descobrir o melhor.
Plantas e animais sempre querem crescer da maneira mais eficiente, e é por isso que a natureza está cheia de padrões matemáticos regulares.
Fibonachos
Até agora, usamos apenas a equação recursiva para números de Fibonacci. Na verdade, também existe uma equação explícita - mas é muito mais difícil encontrar:
Também podemos tentar escolher diferentes pontos de partida para os números de Fibonacci. Por exemplo, se começamos com 2, 1, ... em vez de 1, 1, ... obtemos uma sequência chamada números de Lucas.
Acontece que, quaisquer que sejam os dois números iniciais escolhidos, as seqüências resultantes compartilham muitas propriedades. Por exemplo, as proporções de termos consecutivos sempre
Existem muitos outros quebra-cabeças, padrões e aplicativos relacionados aos números de Fibonacci. Aqui estão alguns exemplos, que você pode experimentar:
Problem solving
1. Divisibilidade de Fibonacci
(a) Quais números de Fibonacci são pares? Existe um padrão para onde eles estão posicionados ao longo da sequência? Você pode explicar o porquê?
(b) Quais números de Fibonacci são divisíveis por 3 (ou divisíveis por 4)? O que você percebe?
2. Soma de Fibonacci
O que acontece se você somar três números consecutivos de Fibonacci? Você pode explicar o porquê?
3. Escadas de Fibonacci
Ao subir as escadas, posso dar um único passo ou pular dois degraus por vez. Isso significa que existem muitas possibilidades diferentes de como eu poderia subir uma escada. Por exemplo, se houver 5 etapas, tenho 8 opções diferentes:
Quantas opções existem para escadas com 6, 7 ou 8 degraus? Você consegue detectar um padrão? E como isso está relacionado aos números de Fibonacci?
© FoxTrot, by Bill Amend